9.6 Tuning the Wrapping Behavior
Wrappable segments are implemented internally using artificial linear elastic forces to draw the knots together and keep them from penetrating obstacles. These artificial forces are invisible to the simulation: the wrapping segment has no mass, and the knot forces are used to create what is essentially a first order physics that “shrink wraps” each segment around the obstacles at the beginning of each simulation step, forming a shortest-distance geodesic curve from which the wrapping contact points A and B are calculated. This process is now described in more detail.
Assume that a wrappable segment has ![]() knots, indexed by
knots, indexed by ![]() , each located at a position
, each located at a position ![]() . Two types of
artificial forces then act on each knot: a wrapping force
that pulls it closer to other knots, and contact forces that
push it away from wrappable obstacles. The wrapping force is given by
. Two types of
artificial forces then act on each knot: a wrapping force
that pulls it closer to other knots, and contact forces that
push it away from wrappable obstacles. The wrapping force is given by
where ![]() is the wrapping stiffness. To determine the contact
forces, we compute, for each wrappable, the knot’s distance to the
surface
is the wrapping stiffness. To determine the contact
forces, we compute, for each wrappable, the knot’s distance to the
surface ![]() and associated normal direction
and associated normal direction ![]() , where
, where ![]() implies that the knot is inside. These quantities are determined
either analytically (for analytic wrappables, Table
9.1), or using a signed distance grid (for
general wrappables, Section 9.3). The
contact forces are then given by
implies that the knot is inside. These quantities are determined
either analytically (for analytic wrappables, Table
9.1), or using a signed distance grid (for
general wrappables, Section 9.3). The
contact forces are then given by
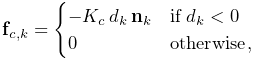 |
where ![]() is the contact stiffness.
is the contact stiffness.
The total force ![]() acting on each knot is then given by
acting on each knot is then given by
where the latter term is the sum of contact forces for all wrappables.
If we let ![]() and
and ![]() denote the aggregate position and force vectors
for all knots, then computing the wrap path involves finding the
equilibrium position such that
denote the aggregate position and force vectors
for all knots, then computing the wrap path involves finding the
equilibrium position such that ![]() . This is done at the
beginning of each simulation step, or whenever updateWrapSegments() is called, and
is achieved iteratively using Newton’s method.
If
. This is done at the
beginning of each simulation step, or whenever updateWrapSegments() is called, and
is achieved iteratively using Newton’s method.
If ![]() and
and ![]() denote the positions and forces at iteration
denote the positions and forces at iteration ![]() ,
and
,
and
denotes the local force derivative (or “stiffness”), then the basic Newton update is given by
In practice, to help deal with the nonlinearities associated with contact, we use a damped Newton update,
| (9.1) |
where ![]() is a constant wrap damping parameter, and
is a constant wrap damping parameter, and ![]() is
an adaptively computed step size adjustment. The computation of
(9.1) can be performed quickly, in
is
an adaptively computed step size adjustment. The computation of
(9.1) can be performed quickly, in ![]() time, since
time, since ![]() is a block-tridiagonal matrix, and the number of
iterations required is typically small (on the order of 10 or less),
particularly since the iterative procedure continues across simulation
steps and so
is a block-tridiagonal matrix, and the number of
iterations required is typically small (on the order of 10 or less),
particularly since the iterative procedure continues across simulation
steps and so ![]() does not need to be brought to
does not need to be brought to ![]() for any given
step. The maximum number of Newton iterations used for each
time step is
for any given
step. The maximum number of Newton iterations used for each
time step is ![]() .
.
Again, it is important to understand the artificial knot forces
described here are separate from the physical spring/muscle tension forces
discussed in Sections 3.1.1 and 4.5.1, and only facilitate the computation of each wrappable segment’s path around obstacles.
The default values for the wrapping parameters are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and these often give
satisfactory results without the need for modification. However, in
some situations the default muscle wrapping may not perform adequately
and it is necessary to adjust these parameters. Problems may include:
, and these often give
satisfactory results without the need for modification. However, in
some situations the default muscle wrapping may not perform adequately
and it is necessary to adjust these parameters. Problems may include:
-
•
The wrapping path does not settle down and tends to “jump around”. Solutions include increasing the damping parameter
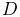 or
the maximum number of wrap iterations
or
the maximum number of wrap iterations 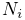 . For general wrapping
surfaces (Section 9.3), one should also
ensure that the surface is sufficiently smooth.
. For general wrapping
surfaces (Section 9.3), one should also
ensure that the surface is sufficiently smooth. -
•
A wrapping surface is too thin and so the wrapping path “jumps through” it. Solutions include increasing the damping parameter
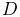 , increasing the number of knots in the segment, or
decreasing the simulation step size. An alternative approach is to use
an alternative wrapping surface
(Section 9.5) that is thicker and
better behaved.
, increasing the number of knots in the segment, or
decreasing the simulation step size. An alternative approach is to use
an alternative wrapping surface
(Section 9.5) that is thicker and
better behaved.
Wrapping parameters are exported as properties of MultiPointSpring and MultiPointMuscle, and may be changed in code (using their set/get accessors), or interactively, either by exposing them through a control panel, or by selecting the spring/muscle in the GUI and choosing Edit properties ... from the right-click context menu. Property values include:
- wrapStiffness
-
Wrapping stiffness
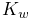 between knot points
(default value 1). Since the wrapping behavior is determined by the
damping to stiffness ratio, it is generally not necessary to
change this value.
between knot points
(default value 1). Since the wrapping behavior is determined by the
damping to stiffness ratio, it is generally not necessary to
change this value. - wrapDamping
-
Damping factor
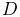 (default
value 10). Increasing this value relative to
(default
value 10). Increasing this value relative to 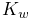 results in wrap
path motions that are smoother and less likely to penetrate obstacles,
but which are also less dynamically responsive. Applications generally
work with damping values between 10 and 100 (assuming
results in wrap
path motions that are smoother and less likely to penetrate obstacles,
but which are also less dynamically responsive. Applications generally
work with damping values between 10 and 100 (assuming 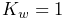 ).
). - contactStiffness
-
Contact stiffness
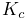 used to resolve obstacle
penetration (default value 10). It is generally not necessary
to change this value. Decreasing it will increase the distance that
knots are permitted to penetrate obstacles, which may result in
a slightly more stable contact behavior.
used to resolve obstacle
penetration (default value 10). It is generally not necessary
to change this value. Decreasing it will increase the distance that
knots are permitted to penetrate obstacles, which may result in
a slightly more stable contact behavior. - maxWrapIterations
-
Maximum number of Newton iterations
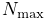 per time step (default value 10). If the wrapping
simulation exhibits instability, particularly with regard to obstacle
contact, increasing the number of iterations (to say 100) may help.
per time step (default value 10). If the wrapping
simulation exhibits instability, particularly with regard to obstacle
contact, increasing the number of iterations (to say 100) may help.
In addition, MultiPointSpring and MultiPointMuscle also export the following properties to control the rendering of knot and A/B points:
- drawKnots
-
If true, renders the knot points in each wrappable segment. This can be useful to visualize the knot density. Knots are rendered using the style, size, and color given by the pointStyle, pointRadius, pointSize, and pointColor values of the spring/muscle’s render properties.
- drawABPoints
-
If true, renders the A/B points. These are the first and last points of contact that a wrap segment makes with each wrappable, and correspond to the points where the spring/muscle’s tension acts on that wrappable (Section 9 and Figure 9.4). A/B points are rendered using the style and size given by the pointStyle, pointRadius (
 ) and pointSize values of the spring/muscle’s render
properties, and the color given by the ABPointColor property.
) and pointSize values of the spring/muscle’s render
properties, and the color given by the ABPointColor property.