8 Contact and Collision 8.6 Overconstrained contact 8.8 Monitoring collisions

8.7 Contact regularization

Contact regularization is a technique in which contact constraints are made “soft” by adding compliance and damping. This means that they no longer remove DOFs from the system, and so overconstraining cannot occur, but contact penetration is no longer strictly enforced and there may be an increase in the computation time required for the simulation.

8.7.1 Compliant contact

Compliant contact is a simple form of regularization that is analogous to that used for joints and connectors, discussed in Section 3.3.8. Compliance and damping parameters and can be specified between any two collidables, with being the inverse of a corresponding contact stiffness , such the contact forces $f_{c}$ acting along each contact normal are given by

$f_{c}=-Kd-D\dot{d},$

(8.1)

where is the contact penetration distance and is negative when penetration occurs. Contact forces act to push the contacting bodies apart, so if body A is penetrating body B and the contact normal ${\bf n}$ is directed toward A, the forces acting on A and B at the contact point will be $f_{c}{\bf n}$ and $-f_{c}{\bf n}$ , respectively. Since is the inverse of the contact stiffness , a value of (the default) implies “infinitely” stiff contact constraints. Compliance is enabled whenever the compliance is set to a value greater than 0, with stiffness decreasing as compliance increases.

Compliance can be enabled by setting the compliance and damping properties of either the collision manager or the CollisionBehavior for a specific collision pair; these properties correspond to and in (8.1). While it is not required to set the damping property, it is usually desirable to set it to a value that approximates critical damping in order to prevent “bouncing” contact behavior. Compliance and damping can be set in the GUI by editing the properties of either the collision manager or a specific collision behavior, or set in code using the accessor methods

⬇

double getCompliance()

void setCompliance (double c)

double getDamping()

void setDamping (double d)

as is illustrated by the following code fragments:

⬇

MechModel mech;

double compliance;

double damping;

... determine compliance and damping values ...

// set damping and compliance for all collisions:

mech.getCollisionManager().setCompliance (compliance);

mech.getCollisionManager().setDamping (damping);

// enable compliance and damping between bodyA and bodyB:

CollisionBehavior behav =

mech.setCollisionBehavior (bodyA, bodyB, true);

behav.setCompliance (compliance);

behav.setDamping (damping);

An important question is what values to choose for compliance and damping. At present, there is no automatic way to determine these, and so some experimental parameter tuning is often necessary. With regard to the contact stiffness , appropriate values will depend on the desired maximum penetration depth and other loadings acting on the body. The mass of the collidable bodies may also be relevant if one wants to control how fast the contact stabilizes. (The mass of every CollidableBody can be determined by its getMass() method.) Since acts on a per-contact basis, the resulting total force will increase with the number of contacts. Once is determined, the compliance value is simply the inverse: .

Given , the damping can then be estimated based on the desired damping ratio $\zeta$ , using the formula

$D=2\zeta\sqrt{KM}$

(8.2)

where is the combined mass of the collidable bodies (or the mass of one body if the other is non-dynamic). Typically, the desired damping will be close to critical damping, for which $\zeta=1$ .

An example that allows a user to play with contact regularization is given in Section 8.5.1.

8.7.2 Contact force behaviors

When regularizing contact through compliance, as described in Section 8.6, the forces $f_{c}$ at each contact are explicitly determined as per (8.1). As a broader alternative to this, ArtiSynth allows applications to specify a contact force behavior, which allows $f_{c}$ to be computed as a more generalized function of :

$f_{c}=-F(d)-D(d)\dot{d},$

(8.3)

where and are functions returning the elastic force and the damping coefficient. The corresponding compliance is then a local function of given by $C(d)=1/F^{\prime}(d)$ (which is the inverse of the local stiffness).

Because is negative during contact, should also be negative. , on the other hand, should be positive, so that the damping acts to reduce $\dot{d}$ .

Figure 8.16: Highly magnified schematic of a single vertex penetration contact between body A (green) and body B (blue). cpnt0 is the point on A penetrating B, while cpnt1 is the corresponding nearest point on the surface of B. The contact normal ${\bf n}$ faces outward from the surface of B towards A, and the penetration distance

is the (negative valued) distance along ${\bf n}$ from cpnt1 to cpnt0.

Contact force behaviors are implemented as subclasses of the abstract class ContactForceBehavior. To enable them, the application sets the forceBehavior property of the CollisionBehavior controlling the contact interaction, using the method

⬇

setForceBehavior (ContactForceBehavior behav)

A ContactForceBehavior must implement the method computeResponse() to compute the contact force, compliance and damping at each contact:

⬇

void computeResponse (

double[] fres, double dist, ContactPoint cpnt0, ContactPoint cpnt1,

Vector3d nrml, double contactArea, int flags);

The arguments to this method supply specific information about the contact (see Figure 8.16):

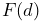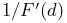fres: An array of length three that returns the contact force, compliance and damping in its first, second and third entries. The contact force is the shown in (8.3), the compliance is $1/F^{\prime}(d)$ ), and the damping is .
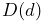dist: The penetration distance 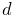(the value of which is negative).
cpnt0, cpnt1: ContactPoint objects containing information about the two points associated with the contact (Figure 8.16), including each point’s position (returned by getPoint()) and associated vertices and weights (returned by numVertices(), getVertices(), and getWeights()).
nrml: The contact normal .
contactArea: Average area per contact, computed by dividing the total area of the contact region by the number of penetrating vertices. This information is only available if the colliderType property of the collision behavior is set to AJL_CONTOUR (Section 8.2.1); otherwise, contactArea will be set to -1.

A collision force behavior may use its computeResponse() method to calculate the force, compliance and damping in any desired way. As per equation (8.3), these quantities are functions of the penetration distance , supplied by the argument dist.

A very simple instance of ContactForceBehavior that just recreates the contact compliance of (8.1) is shown below:

⬇

class SimpleCompliantContact extends ContactForceBehavior {

double myStiffness = 10000.0; // contact stiffness

double myDamping = 10.0;

public void computeResponse (

double[] fres, double dist, ContactPoint cpnt0, ContactPoint cpnt1,

Vector3d nrml, double regionArea, int flags) {

fres[0] = dist*myStiffness; // contact force

fres[1] = 1/myStiffness // compliance is inverse of stiffness

fres[2] = myDamping; // damping

}

This example uses only the penetration distance information supplied by dist, dividing it by the compliance to determine the contact force. Since dist is negative when the collidables are interpenetrating, the returned contact force will also be negative.

8.7.2.1 Computing forces based on pressure

Often, such as when implementing elastic foundation contact (Section 8.7.3), the contact force behavior is expressed in terms of pressure, given as a function of :

(8.4)

In that case, the contact force is determined by multiplying by the local area associated with the contact:

$F(d)=A\,G(d).$

(8.5)

Since and are both assumed to be negative during contact, we will assume here that is negative as well.

To find the area within the computeResponse() method, one has two options:

A)

Compute an estimate of the local contact area surrounding the contact, as discussed below. This may be the more appropriate option if the colliding mesh vertices are not uniformly spaced, or if the contactArea argument is undefined because the AJL_CONTOUR collider (Section 8.4.2) is not being used.
B)

Use the contactArea argument if it is is defined. This gives an accurate estimate of the per-contact area on the assumption that the colliding mesh vertices are uniformly distributed. contactArea will be defined when using the AJL_CONTOUR collider (Section 8.4.2); otherwise, it will be set to -1.

For option (A), ContactForceBehavior provides the convenience method computeContactArea(cpnt0,cpnt1,nrml), which estimates the local contact area given the contact points and normal. If the above example of computeResponse() is modified so that the stiffness parameter controls pressure instead of force, then we obtain the following:

⬇

public void computeResponse (

double[] fres, double dist, ContactPoint cpnt0, ContactPoint cpnt1,

Vector3d nrml, double regionArea, int flags) {

// assume stiffness determines pressure instead of force,

// so it needs to be scaled by the local contact area:

double K = myStiffness * computeContactArea (cpnt0, cpnt1, nrml);

fres[0] = dist*K; // contact force

fres[1] = 1/K; // compliance

fres[2] = myDamping; // damping

}

computeContactArea() only works for vertex penetration contact (Section 8.4.1.2), and will return -1 otherwise. That’s because it needs the contact points’ vertex information to compute the area. In particular, for vertex penetration contact, it associates the vertex with 1/3 of the area of each of its surrounding faces.

When computing contact forces, care must also be taken to consider whether the vertex penetrations are being computed for both colliding surfaces (two-way contact, Section 8.4.1.2). This means that forces are essentially being computed twice - once for each side of the penetrating surface. For forces based on pressure, the resulting contact forces should then be halved. To determine when two-way contact is in effect, the flags argument can be examined for the flag TWO_WAY_CONTACT:

⬇

public void computeResponse (

double[] fres, double dist, ContactPoint cpnt0, ContactPoint cpnt1,

Vector3d nrml, double regionArea, int flags) {

double K = myStiffness * computeContactArea (cpnt0, cpnt1, nrml);

if ((flags & TWO_WAY_CONTACT) != 0) {

K *= 0.5; // divide force response by 2

}

fres[0] = dist*K; // contact force

fres[1] = 1/K; // compliance

fres[2] = myDamping; // damping

}

8.7.3 Elastic foundation contact

ArtiSynth supplies a built-in contact force behavior, LinearElasticContact, that implements elastic foundation contact (EFC) based on a linear material law as described in [3]. By default, the contact pressures are computed from

$G(d)=-\frac{(1-\nu)E}{(1+\nu)(1-2\nu)}\ln\left(1+\frac{d}{h}\right),$

(8.6)

where is Young’s modulus, $\nu$ is Poisson’s ratio, is the contact penetration distance, and is the foundation layer thickness. (Note that both and are negated relative to the formulation in [3] because we assume during contact.) The use of the $\ln()$ function helps ensure that contact does not penetrate the foundation layer. However, to ensure robustness in case contact does penetrate the layer (or comes close to doing so), the pressure relationship is linearized (with a steep slope) whenever , where is the minimum thickness ratio controlled by the LinearElasticContact property minThicknessRatio.

Alternatively, if a strictly linear pressure relationship is desired, this can be achieved by setting the property useLogDistance to false. The pressure relationship then becomes

$G(d)=\frac{(1-\nu)E}{(1+\nu)(1-2\nu)}\left(\frac{d}{h}\right),$

(8.7)

where again will be negative when .

Damping forces $f_{d}=-D(d)\dot{d}$ can be computed in one of two ways: either with set to a constant such that

$f_{d}=-C\dot{d},$

(8.8)

or with set to a multiple of and the magnitude of the elastic contact force , such that

$f_{d}=-C|F(d)|\dot{d}.$

(8.9)

The latter is compatible with the EFC damping used by OpenSim (equation 24 in [22]).

Elastic foundation contact assumes the use of vertex penetration contact (Section 8.4.1) to achieve correct results; otherwise, a runtime error may result.

LinearElasticContact exports several properties to control the force response described above:

youngsModulus: in equations (8.7) and (8.6).
poissonsRatio: $\nu$ in equations (8.7) and (8.6).
thickness: in equations (8.7) and (8.6).
minThicknessRatio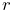: value such that (8.6) is linearized if 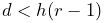. The default value is 0.01.
dampingFactor: in equations (8.8) and (8.9).
dampingMethod: An enum of type ElasticContactBase.DampingMethod, for which DIRECT and FORCE cause damping to be implemented using (8.8) and (8.9), respectively. The default value is DIRECT.
useLogDistance: A boolean, which if true causes (8.6) to be used instead of (8.7). The default value is true.
useLocalContactArea: A boolean, which if true causes contact areas to be estimated from the vertex of the penetrating contact point (option A in Section 8.7.2.1). The default value is true.

8.7.4 Example: elastic foundation contact of a ball in a bowl

A simple example of elastic foundation contact is defined by the model

  artisynth.demos.tutorial.ElasticFoundationContact

This implements EFC between a spherical ball and a bowl into which it is dropped. Pressure rendering is enabled (Section 8.5.3), and the bowl is made transparent, allowing the contact pressure to be viewed as the ball moves about.

Figure 8.17: ElasticFoundationContact showing contact pressure between the ball and bowl during contact.

The source code for the build method is shown below:

⬇

1 public void build (String[] args) throws IOException {

2 MechModel mech = new MechModel ("mech");

3 mech.setGravity (0, 0, -9.8);

4 addModel (mech);

6 // read in the mesh for the bowl

7 PolygonalMesh mesh = new PolygonalMesh (

8 PathFinder.getSourceRelativePath (

9 ElasticFoundationContact.class, "data/bowl.obj"));

11 // create the bowl from the mesh and make it non-dynamic

12 RigidBody bowl =

13 RigidBody.createFromMesh (

14 "bowl", mesh, /*density=*/1000.0, /*scale=*/1.0);

15 mech.addRigidBody (bowl);

16 bowl.setDynamic (false);

18 // create another spherical mesh to define the ball

19 mesh = MeshFactory.createIcosahedralSphere (0.7, 3);

20 // create the ball from the mesh

21 RigidBody ball =

22 RigidBody.createFromMesh (

23 "ball", mesh, /*density=*/1000.0, /*scale=*/1.0);

24 // move the ball into an appropriate "drop" position

25 ball.setPose (new RigidTransform3d (0.1, 0, 0));

26 mech.addRigidBody (ball);

28 // Create a collision behavior that uses EFC. Set friction

29 // to 0.1 so that the ball will actually roll.

30 CollisionBehavior behav = new CollisionBehavior (true, 0.1);

31 behav.setMethod (Method.VERTEX_PENETRATION); // needed for EFC

32 // create the EFC and set it in the behavior

33 LinearElasticContact efc =

34 new LinearElasticContact (

35 /*E=*/100000.0, /*nu=*/0.4, /*damping=*/0.1, /*thickness=*/0.1);

36 behav.setForceBehavior (efc);

38 // set the collision behavior between the ball and bowl

39 mech.setCollisionBehavior (ball, bowl, behav);

41 // contact rendering: render contact pressures

42 CollisionManager cm = mech.getCollisionManager();

43 cm.setDrawColorMap (ColorMapType.CONTACT_PRESSURE);

44 RenderProps.setVisible (cm, true);

45 // mesh rendering: render only edges of the bowl so we can see through it

46 RenderProps.setFaceStyle (bowl, FaceStyle.NONE);

47 RenderProps.setLineColor (bowl, new Color (0.8f, 1f, 0.8f));

48 RenderProps.setDrawEdges (mech, true); // draw edges for all meshes

49 RenderProps.setFaceColor (ball, new Color (0.8f, 0.8f, 1f));

51 // create a panel to allow control over some of the force behavior

52 // parameters and rendering properties

53 ControlPanel panel = new ControlPanel("options");

54 panel.addWidget (behav, "forceBehavior");

55 panel.addWidget (behav, "friction");

56 panel.addWidget (cm, "colorMapRange");

57 addControlPanel (panel);

58 }

The demo first creates the ball and the bowl as rigid bodies (lines 6-26), with the bowl defined by a mesh read from the file data/bowl.obj relative to the demo source directory, and the ball defined as an icosahedral sphere. The bowl is fixed in place (bowl.setDynamic(false)), and the ball is positioned at a suitable location for dropping into the bowl when simulation begins.

Next, a collision behavior is created, with its collision method property set to VERTEX_PENETRATION (as required for EFC), and a friction coefficient of 0.1 (to ensure that the ball will actually roll) (lines 28-31). A LinearElasticContact is then constructed, with $E=10^{5}$ , $\nu=0.4$ , damping factor , and thickness , and added to the collision behavior using setForceBehavior() (lines 32-26). The behavior is then used to enable contact between the ball and bowl (line 39).

Lines 41-49 set up rendering properties: the collision manager is made visible, with color map rendering set to CONTACT_PRESSURE, and the ball and bowl are set to be rendered in pale blue and green, with the bowl rendered using only mesh edges so as to make it transparent.

Finally, a control panel is created allowing the user to adjust properties of the contact force behavior and the pressure rendering range (lines 51-57).

To run this example in ArtiSynth, select All demos > tutorial > ElasticFoundationContact from the Models menu. Running the model will cause the ball to drop into the bowl, with the resulting contact pressures rendered as in Figure 8.17.

8.7.5 Example: binding EFC properties to fields

It is possible to bind certain EFC material properties to a field, for situations where these properties vary over the surface of the contacting meshes. Properties of LinearElasticContact that can be bound to (scalar) fields include YoungsModulus and thickness, using the methods

⬇

setYoungsModulusField (ScalarFieldComponent fcomp)

setThicknessField (ScalarFieldComponent fcomp)

Most typically, the properties will be bound to a mesh field (Section 7.3) defined with respect to one of the colliding meshes.

When determining the value of either youngsModulus or thickness within its computeResponse() method, LinearElasticContact checks to see if the property is bound to a field. If it is, the method first checks if the field is a mesh field associated with the meshes of either cpnt0 or cpnt1, and if so, extracts the value using the vertex information of the associated contact point. Otherwise, the value is extracted from the field using the position of cpnt0.

A simple example of binding the thickness property to a field is given by

  artisynth.demos.tutorial.VariableElasticContact

This implements EFC between a beveled cylinder and a plate on which it is resting. The plate is made transparent, allowing the contact pressure to be viewed from below.

Figure 8.18: VariableElasticContact showing the contact pressure decreasing radially from the cylinder center, as the EFC thickness property increases due to its field binding (left). Without the field binding, the thickness and the pressure are constant across the cylinder bottom (right).

The model’s code is similar to that for ElasticFoundationContact (Section 8.7.4), except that the collidables are different and the EFC thickness property is bound to a field. The source code for the first part of the build method is shown below:

⬇

1 public void build (String[] args) throws IOException {

2 MechModel mech = new MechModel ("mech");

3 mech.setGravity (0, 0, -9.8);

4 addModel (mech);

6 // read in the mesh for the top cylinder

7 PolygonalMesh mesh = new PolygonalMesh (

8 PathFinder.getSourceRelativePath (

9 VariableElasticContact.class, "data/beveledCylinder.obj"));

10 // create the cylinder from the mesh

11 RigidBody cylinder =

12 RigidBody.createFromMesh (

13 "cylinder", mesh, /*density=*/1000.0, /*scale=*/1.0);

14 mech.addRigidBody (cylinder);

16 // create a plate from a box mesh and make it non-dynamic

17 RigidBody plate =

18 // box has widths 1.5 x 1.5 x 0.5 and mesh resolutions 10 x 10 x 4

19 RigidBody.createBox (

20 "plate", 1.5, 1.5, 0.5, 10, 10, 4, /*density=*/1000.0, false);

21 plate.setPose (new RigidTransform3d (0, 0, -0.75));

22 plate.setDynamic (false);

23 mech.addRigidBody (plate);

25 // enable vertex penetrations (required by EFC)

26 CollisionManager cm = mech.getCollisionManager();

27 cm.setMethod (Method.VERTEX_PENETRATION);

28 // create the EFC

29 double thickness = 0.1;

30 LinearElasticContact efc =

31 new LinearElasticContact (

32 /*E=*/100000.0, /*nu=*/0.4, /*damping=*/0.1, thickness);

34 // Create a thickness field for the cylinder mesh. Use a scalar vertex

35 // field, with the thickness value h defined by h = thickness * (1 + r),

36 // where r is the radial distance from the cylinder axis.

37 ScalarVertexField field =

38 new ScalarVertexField (cylinder.getSurfaceMeshComp());

39 for (Vertex3d vtx : mesh.getVertices()) {

40 Point3d pos = vtx.getPosition();

41 double r = Math.hypot (pos.x, pos.y);

42 field.setValue (vtx, thickness*(1+r));

43 }

44 // add the field to the MechModel, and bind the EFC thickness property

45 mech.addField (field);

46 efc.setThicknessField (field);

48 // create a collision behavior that uses the EFC

49 CollisionBehavior behav = new CollisionBehavior (true, /*friction=*/0.1);

50 // Important: call setForceBehavior() *after* properties have been bound

51 behav.setForceBehavior (efc);

52 // enable cylinder/plate collisions using the behavior

53 mech.setCollisionBehavior (cylinder, plate, behav);

First, the cylinder and the plate are created as rigid bodies (lines 6-23), with the cylinder defined by a mesh read from the file data/beveledCylinder.obj relative to the demo source directory. The plate is fixed in place and positioned so that it is directly under the cylinder.

Next, the contact method is set to VERTEX_PENETRATION (as required for EFC), this time by setting it for all collisions in the collision manager, and a LinearElasticContact is constructed, with $E=10^{5}$ , $\nu=0.4$ , damping factor , and thickness (lines 25-32). Then in lines 34-43, a ScalarMeshField is created for the cylinder surface mesh, with vertex values set so that the field defines a thickness value that increases with the radial distance from the cylinder axis according to:

$h=\text{thickness}\;(1+r)$

This field is then added to the fields list of the MechModel and the EFC thickness property is bound to it (lines 44-46).

Lastly, a collision behavior is created, with the EFC added to it as a force behavior, and used to enable cylinder/plate collisions (lines 48-53).

It is important that EFC properties are bound to fields before the behavior method setForceBehavior() is called, because that method copies the force behavior and so subsequent field bindings would not be noticed. If for some reason the bindings must be made after the call, they should be applied to the copied force behavior, which can be obtained using getForceBehavior().

To run this example in ArtiSynth, select All demos > tutorial > VariableElasticContact from the Models menu. Running the model will result in contact pressures seen in the left of Figure 8.18, with the pressures decreasing radially in response to the increasing thickness. With no field binding, the pressures are constant across the cylinder bottom (Figure 8.18, right).

8.6 Overconstrained contact Bibliography 8.8 Monitoring collisions

Generated on Wed Jul 24 21:23:12 2024 by LaTeXML [LOGO]