6.11 Stress, strain and strain energy
An ArtiSynth FEM model has the capability to compute a variety of stress and strain measures at each of its nodes, as well as strain energy for each element and for the entire model.
6.11.1 Computing nodal values
Stress, strain, and strain energy density can be computed at each node of an FEM model. By default, these quantities are not computed, in order to conserve computing power. However, their computation can be enabled with the FemModel3d properties computeNodalStress, computeNodalStrain and computeNodalEnergyDensity, which can be set either in the GUI, or using the following accessor methods:
| void setComputeNodalStress(boolean) |
Enable stress to be computed at each node. |
| boolean getComputeNodalStress() |
Queries if nodal stress computation enabled. |
| void setComputeNodalStrain(boolean) |
Enable strain to be computed at each node. |
| boolean getComputeNodalStrain() |
Queries if nodal strain computation enabled. |
| void setComputeNodalEnergyDensity(boolean) |
Enable strain energy density to be computed at each node. |
| boolean getComputeNodalEnergyDensity() |
Queries if nodal strain energy density computation enabled. |
Setting these properties to true will cause their respective values to be computed at the nodes during each subsequent simulation step. This is done by computing values at the element integration points, extrapolating these values to the nodes, and then averaging them across the contributions from all surrounding elements.
Once computed, the values may be obtained at each node using the following FemNode3d methods:
| SymmetricMatrix3d getStress() |
Returns the current Cauchy stress at the node. |
| SymmetricMatrix3d getStrain() |
Returns the current strain at the node. |
| double getEnergyStrain() |
Returns the current strain energy density at the node. |
The stress value is the Cauchy stress. The strain values depend on the
primary material within each element: if the material is linear,
strain will be the small deformation Cauchy strain (co-rotated if the
material’s corotated property is true), while otherwise it
will be Green strain ![]() :
:
| (6.39) |
where ![]() is the right Cauchy-Green tensor.
is the right Cauchy-Green tensor.
6.11.2 Scalar stress/strain measures
Stress or strain values are tensor quantities represented by symmetric
![]() matrices. If they are being computed at the nodes, a
variety of scalar quantities can be extracted from them, using the
FemNode3d method
matrices. If they are being computed at the nodes, a
variety of scalar quantities can be extracted from them, using the
FemNode3d method
| double getStressStrainMeasure(StressStrainMeasure m) |
where StressStrainMeasure is an enumerated type with the following entries:
- VonMisesStress
-
von Mises stress, equal to
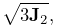
where
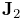 the second invariant of the average deviatoric stress.
the second invariant of the average deviatoric stress. - MAPStress
-
Absolute value of the maximum principle Cauchy stress.
- MaxShearStress
-
Maximum shear stress, given by
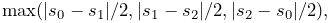
where
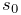 ,
, 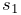 and
and 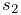 are the eigenvalues of the stress tensor.
are the eigenvalues of the stress tensor. - VonMisesStrain
-
von Mises strain, equal to
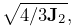
where
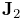 the second invariant of the average deviatoric strain.
the second invariant of the average deviatoric strain.
- MAPStrain
-
Absolute value of the maximum principle strain.
- MaxShearStrain
-
Maximum shear strain, given by
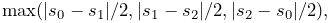
where
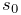 ,
, 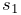 and
and 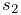 are the eigenvalues of the strain tensor.
are the eigenvalues of the strain tensor. - EnergyDensity
-
Strain energy density.
These quantities can also be queried with the following convenience methods:
| double getVonMisesStress() |
Return the von Mises stress. |
| double getMAPStress() |
Return the maximum absolute principle stress. |
| double getMaxShearStress() |
Return the maximum shear stress. |
| double getVonMisesStrain() |
Return the von Mises strain. |
| double getMAPStrain() |
Return the maximum absolute principle strain. |
| double getMaxShearStrain() |
Return the maximum shear strain. |
| double getEnergyDensity() |
Return the strain energy density. |
For muscle-activated FEM materials, strain energy density is currently computed only for the passive portions of the material; no energy density is computed for the stress component that depends on muscle activation.
As indicated above, extracting these measures requires that the appropriate underling quantity (stress, strain or strain energy density) is being computed at the nodes; otherwise, 0 will be returned. To ensure that the appropriate underlying quantity is being computed for a specific measure, one may use the FemModel3d method
| void setComputeNodalStressStrain (StressStrainMeasure m) |
6.11.3 Strain energy
Strain energy density can be integrated over an FEM model’s volume to compute a total strain energy. Again, to save computational resources, this must be explicitly enabled using the FemModel3d property computeStrainEnergy, which can be set either in the GU or using the accessor methods:
| void setComputeStrainEnergy(boolean) |
Enable strain energy computation. |
| boolean getComputeStrainEnergy() |
Queries strain energy computation. |
Once computation is enabled, strain energy is exported for the entire model using the read-only strainEnergy property, which can be accessed using
| double getStrainEnergy() |
The FemElement method getStrainEnergy() returns the strain energy for individual elements.