A Mathematical Review A.2 Rigid transforms A.4 Rotational velocity

A.3 Affine transforms

An affine transform is a generalization of a rigid transform, in which the rotational component ${\bf R}$ is replaced by a general $3\times 3$ matrix ${\bf A}$ . This means that an affine transform implements a generalized basis transformation combined with an offset of the origin (Figure A.7). As with ${\bf R}$ for rigid transforms, the columns of ${\bf A}$ still describe the transformed basis vectors ${\bf x}^{\prime}$ , ${\bf y}^{\prime}$ , and ${\bf z}^{\prime}$ , but these are generally no longer orthonormal.

Figure A.7: A position vector ${\bf p}_{BA}$ and a general matrix ${\bf A}_{BA}$ describing the affine position and basis transform of frame B with respect to frame A.

Expressed in terms of homogeneous coordinates, the affine transform ${\bf X}_{AB}$ takes the form

${\bf X}_{BA}=\left(\begin{matrix}{\bf A}_{BA}&{\bf p}_{BA}\\ 0&1\end{matrix}\right)$

(A.18)

with

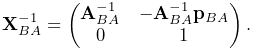${\bf X}_{BA}^{-1}=\left(\begin{matrix}{\bf A}_{BA}^{-1}&-{\bf A}_{BA}^{-1}{\bf p% }_{BA}\\ 0&1\end{matrix}\right).$

(A.19)

As with rigid transforms, when an affine transform is applied to a vector instead of a point, only the matrix ${\bf A}$ is applied and the translation component ${\bf p}$ is ignored.

Affine transforms are typically used to effect transformations that require stretching and shearing of a coordinate frame. By the polar decomposition theorem, ${\bf A}$ can be factored into a regular rotation ${\bf R}$ plus a symmetric shearing/scaling matrix ${\bf P}$ :

${\bf A}={\bf R}\,{\bf P}$

(A.20)

Affine transforms can also be used to perform reflections, in which ${\bf A}$ is orthogonal (so that ${\bf A}^{T}\,{\bf A}={\bf I}$ ) but with $\det{\bf A}=-1$ .

A.2 Rigid transforms Bibliography A.4 Rotational velocity

Generated on Sun Jan 12 23:00:57 2025 by LaTeXML [LOGO]