A.1 Rotation transforms
Rotation matrices are used to describe the orientation of 3D coordinate frames in space, and to transform vectors between these coordinate frames.

Consider two 3D coordinate frames A and B that are rotated with
respect to each other (Figure A.1). The orientation
of B with respect to A can be described by a ![]() rotation
matrix
rotation
matrix ![]() , whose columns are the unit vectors giving the
directions of the rotated axes
, whose columns are the unit vectors giving the
directions of the rotated axes ![]() ,
, ![]() , and
, and ![]() of B with
respect to A.
of B with
respect to A.
![]() is an orthogonal matrix, meaning that
its columns are both perpendicular and mutually
orthogonal, so that
is an orthogonal matrix, meaning that
its columns are both perpendicular and mutually
orthogonal, so that
| (A.1) |
where ![]() is the
is the ![]() identity matrix. The inverse
of
identity matrix. The inverse
of ![]() is hence equal to its transpose:
is hence equal to its transpose:
| (A.2) |
Because ![]() is orthogonal,
is orthogonal, ![]() , and because it
is a rotation,
, and because it
is a rotation, ![]() (the other case, where
(the other case, where ![]() , is not a rotation but a reflection). The 6 orthogonality
constraints associated with a rotation matrix mean that in spite of
having 9 numbers, the matrix only has 3 degrees of freedom.
, is not a rotation but a reflection). The 6 orthogonality
constraints associated with a rotation matrix mean that in spite of
having 9 numbers, the matrix only has 3 degrees of freedom.
Now, assume we have a 3D vector ![]() , and consider its coordinates
with respect to both frames A and B. Where necessary, we use a
preceding superscript to indicate the coordinate frame with respect to
which a quantity is described, so that
, and consider its coordinates
with respect to both frames A and B. Where necessary, we use a
preceding superscript to indicate the coordinate frame with respect to
which a quantity is described, so that ![]() and
and ![]() and
denote
and
denote ![]() with respect to frames A and B, respectively. Given the
definition of
with respect to frames A and B, respectively. Given the
definition of ![]() given above, it is fairly straightforward to
show that
given above, it is fairly straightforward to
show that
| (A.3) |
and, given (A.2), that
| (A.4) |
Hence in addition to describing the orientation of B with respect to A,
![]() is also a transformation matrix that maps vectors in B
to vectors in A.
is also a transformation matrix that maps vectors in B
to vectors in A.
It is straightforward to show that
| (A.5) |

A simple rotation by an angle ![]() about one of the basic
coordinate axes is known as a basic rotation. The three
basic rotations about x, y, and z are:
about one of the basic
coordinate axes is known as a basic rotation. The three
basic rotations about x, y, and z are:
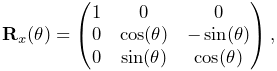 |
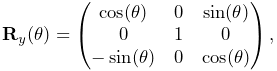 |
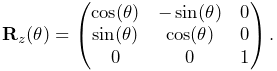 |
Next, we consider transform composition. Suppose we have three
coordinate frames, A, B, and C, whose orientation are related to each other by
![]() ,
, ![]() , and
, and ![]() (Figure
A.6). If we know
(Figure
A.6). If we know ![]() and
and ![]() ,
then we can determine
,
then we can determine ![]() from
from
| (A.6) |
This can be understood in terms of vector transforms. ![]() transforms a vector from C to B, which is equivalent to first
transforming from C to A,
transforms a vector from C to B, which is equivalent to first
transforming from C to A,
| (A.7) |
and then transforming from A to B:
| (A.8) |
Note also from (A.5) that ![]() can be
expressed as
can be
expressed as
| (A.9) |
In addition to specifying rotation matrix components explicitly, there are numerous other ways to describe a rotation. Three of the most common are:
- Roll-pitch-yaw angles
-
There are 6 variations of roll-pitch-yaw angles. The one used in ArtiSynth corresponds to older robotics texts (e.g., Paul, Spong) and consists of a roll rotation
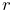 about the z axis, followed by a pitch
rotation
about the z axis, followed by a pitch
rotation 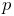 about the new y axis, followed by a yaw rotation
about the new y axis, followed by a yaw rotation 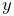 about the new x axis. The net rotation can be expressed by the
following product of basic rotations:
about the new x axis. The net rotation can be expressed by the
following product of basic rotations: 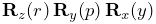 .
. - Axis-angle
-
An axis angle rotation parameterizes a rotation as a rotation by an angle
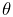 about a specific axis
about a specific axis 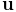 . Any rotation
can be represented in such a way as a consequence of Euler’s rotation
theorem.
. Any rotation
can be represented in such a way as a consequence of Euler’s rotation
theorem. - Euler angles
-
There are 6 variations of Euler angles. The one used in ArtiSynth consists of a rotation
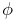 about the z axis, followed by a rotation
about the z axis, followed by a rotation
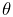 about the new y axis, followed by a rotation
about the new y axis, followed by a rotation 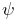 about the
new z axis. The net rotation can be expressed by the following product
of basic rotations:
about the
new z axis. The net rotation can be expressed by the following product
of basic rotations: 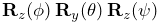 .
.